The Thermodynamic Modeling of Multicomponent Phase Equilibria. Ursula R. Kattner.

Author's Note: In this article, commercial products are identified as examples. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that they are necessarily the best available for the purpose. Enormous progress has been made in the calculation of phase diagrams during the past 3. This progress will continue as model descriptions are improved and computational technology advances.

• This over-simplified one-line diagram of a power distribution system included values necessary for working through the two methods of short-circuit calculation.
• While the the first calculation method proposed is the simplest, I’m not sure it’s the fairest the phases aren’t one big bucket of energy – there’s three.
• In power engineering, the power-flow study, or load-flow study, is a numerical analysis of the flow of electric power in an interconnected system.
• A phase shifting transformer (see fig.1) is a special type of system intertie transformers which Control the power flow through specific lines in a complex power.

Phase Diagram Calculation Programs For Weddings

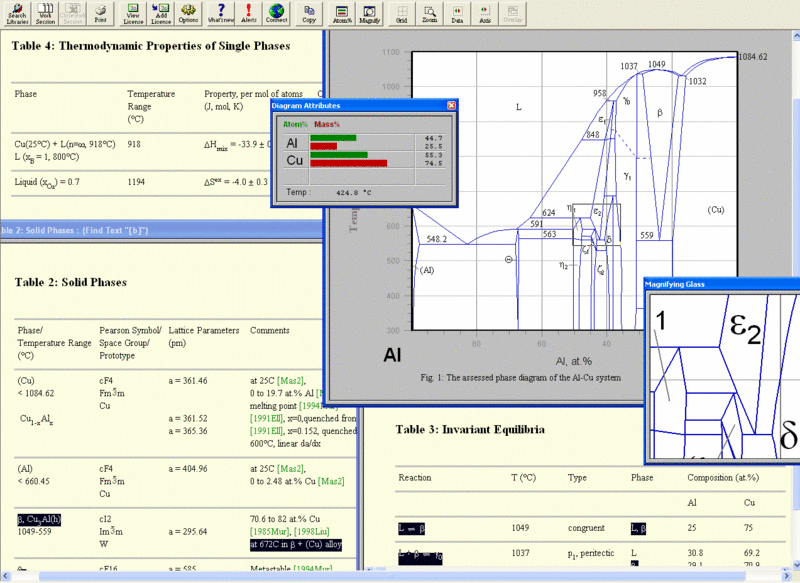
Improvement has been made in the model descriptions in the CALPHAD method, the coupling of phase diagrams with kinetic process modeling, computer programs for easy access to phase diagram information, and the construction of databases used for calculating the phase diagrams of complex commercial alloys. The importance of phase diagrams is also reflected by the publication of such handbooks as Binary Alloy Phase Diagrams,1. Phase Equilibria, Crystallographic and Thermodynamic Data of Binary Alloys,2. Phase Equilibrium Diagrams,3 which continues in Phase Diagrams for Ceramists,4. Handbook of Ternary Alloy Phase Diagrams,5 and Ternary Alloys. The state of a two- component material at constant pressure can be presented in the well- known graphical form of binary phase diagrams.

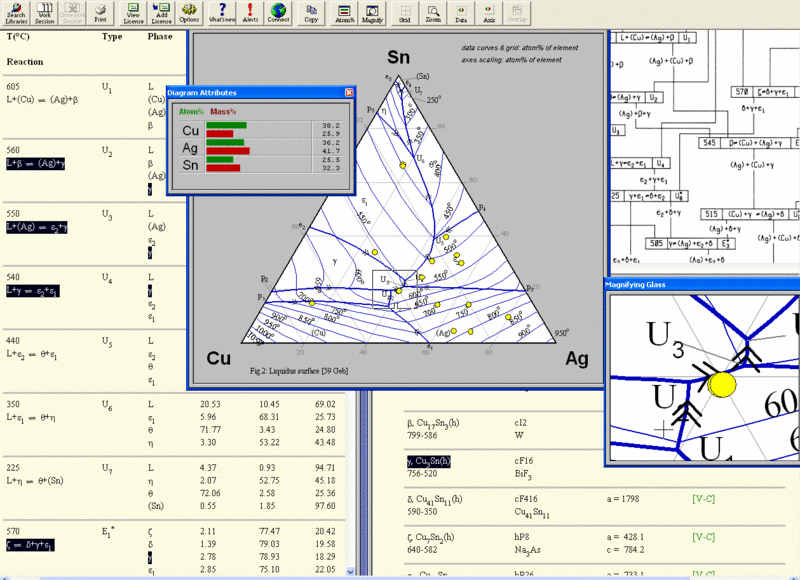
For three- component materials, an additional dimension is necessary for a complete representation. Therefore, ternary systems are usually presented by a series of sections or projections. Due to their multidimensionality, the interpretation of the diagrams of more complex systems can be quite cumbersome for an occasional user of these diagrams. For systems with more than three components, the graphical representation of the phase diagram in a useful form becomes not only a challenging task, but is also hindered by the lack of sufficient experimental information.

However, the difficulty of graphically representing systems with many components is irrelevant for the calculation of phase diagrams; such calculations can be customized for the materials problem of interest. To describe the solution phases, van Laar used concentration dependent terms that Hildebrand.

More than 4. 0 years had passed when J. L. Meijering published his calculations of miscibility gaps in ternary.

Shortly afterward, Meijering applied this method to the thermodynamic analysis of the Cr- Cu- Ni system. Simultaneously, Kaufman and Cohen. Fe- Ni system; Kaufman continued his work on the calculation of phase diagrams, including pressure dependence.

Just wondering which method do you think the most accurate for calculating single phase-earth faults, the Ohmic Method or Symmetrical Component Method. Siw Keygen Download For Hex.

Prode Properties Properties of pure fluids and mixtures, multi phase equilibria, process simulation, software. Title : phase envelope, diagram, curve, curves, natural. Use Google Drive to make online shareable electric circuit diagrams. PLC (Programmable Logic Controllers) are widely used in industrial and manufacturing automation systems for improved operational availability and extendable.

Phase Diagram Calculation Programs For Troubled

In 1. 97. 0, Kaufman and Bernstein. CALPHAD method (CALculation of PHAse Diagrams). In 1. 97. 3, Kaufman organized the first project meeting of the international CALPHAD group.

Since then, the CALPHAD group has grown consistently larger. In his paper, Kikuchi. This method later became known as the cluster variation method (CVM) and is extensively used in conjunction with first- principles calculations. Although these calculations are computationally very intensive, enormous progress in algorithms and computer speed has been made in recent years. The predicted phase diagrams are generally topologically correct, but they currently lack sufficient accuracy for practical applications.

De Fontaine. 16 gives an extensive review of these calculations. The assessed excess Gibbs energies of the constituent subsystems are for extrapolation to a higher component system. With stainless steel alloys, for example, the complexity is frequently reduced by expressing the compositions of the ferrite- stabilizing elements as chromiumequivalents and the austenite- stabilizing elements as nickel equivalents. The sums of the chromium and nickel equivalents are used to predict the phases expected in the final alloy. It should be noted that approximations like these are limited to the composition regime for which they were derived. Another example is the PHACOMP method.

TCP) phases in superalloys. This method is based on the theory that each element has a specific electron hole number, and the average electron hole number is correlated to the TCP phases in an alloy. Although this method works very well for nickel- based superalloys, special corrections are required with other superalloys, and it may not be easily applied to other alloy families. The CALPHAD method, on the other hand, is based on the minimization of the free energy of the system and is, thus, not only completely general and extensible, but also theoretically meaningful. This becomes even more pronounced as the number of components increases. The calculation of phase diagrams reduces the effort required to determine equilibrium conditions in a multicomponent system. A preliminary phase diagram can be obtained from extrapolation of the thermodynamic functions of constituent subsystems.

This preliminary diagram can be used to identify composition and temperature regimes where maximum information can be obtained with minimum experimental effort. This information can then be used to refine the original thermodynamic functions. Even though phase diagrams represent thermodynamic equilibrium, it is well established that the phase equilibria can be applied locally (local equilibrium) to describe the interfaces between phases. In such cases, only the concentrations at this interface are assumed to obey the requirements of thermodynamic equilibrium.

Thermodynamic modeling of phase diagrams and kinetic modeling have been successfully coupled for a variety of processes, such as carburizing/nitriding,1. Phase- equilibrium calculations can not only give the phases present and their compositions, but can also provide numerical values of enthalpy contents, temperature, and concentration dependence of phase boundaries for coupling of microscopic and macroscopic modeling. Banerjee et al. 2.

The CALPHAD method employs a variety of models to describe the temperature, pressure, and concentration dependencies of the free- energy functions of the various phases. The contributions to the Gibbs energy of a phase j can be written as.

Gibbs energy by the temperature (T) and the composition (x), is the contribution of the pressure (p), and is the magnetic contribution of the Curie or N. To represent the pure elements, the n are typically 2, 3, - 1, and 7 or - 9. This function is valid for temperatures above the Debye temperature; in each of the equations in the following models describing the concentration dependence, the G coefficients on the right- hand side can have such a temperature dependence. Frequently, only the first two terms are used for the representation of the excess Gibbs energy. Dinsdale. 29 also gives expressions for the effects of pressure and magnetism on the Gibbs energy; however, pressure dependence for condensed systems at normal pressures is usually ignored. Since Hildebrand. For example, an ionic liquid model.

For ordered solid phases, Wagner and Schottky. Today, the most commonly used models (listed in order of increasing complexity) are those for stoichiometric phases, regular solution- type models for disordered phases, and sublattice models for ordered phases having a range of solubility or exhibiting an order/disorder transformation. The following examples give descriptions of models for binary phases and can easily be expanded for ternary and higher order phases. The first two terms correspond to G0, and the third term corresponds to Gxs in Equation 4.

Gideal of Equation 4 is zero for a stoichiometric phase, since there is no random mixing. The first two terms correspond to G0 and the third term, from random mixing, to Gideal in Equation 4. The Gi of the fourth term are coefficients of the excess Gibbs energy term, Gxs, in Equation 4.

The sum of the terms (x. A - x. B)i is the so- called Redlich- Kister polynomial,3. Although other polynomials have been used in the past, in most cases they can be converted to Redlich- Kister polynomials.